« Regularization for Machine Learning Models

A common problem in machine learning is overfitting, where a model falsely generalizes noise in the training data:

A popular approach to remedy this problem and make the model more robust is regularization: A penalty term is added to the algorithm’s loss function. This changes the model’s weights which result from minimizing the loss function.

The most popular regularization techniques are Lasso, Ridge (aka Tikhonov) and Elastic Net. For the exemplary case of simple linear regression with only one weight parameter w (the slope of the linear fit), their penalty terms look like this (including a scaling parameter λ):

• Lasso (L1): λ·|w|
• Ridge (L2): λ·w²
• Elastic Net (L1+L2): λ₁·|w| + λ₂·w²

The different terms have different effects: Compared to L1, the quadratic L2 regularization becomes negligible at small weights (close to zero), but stronger at large weights. This leads to the following behaviours, casually phrased:

• Linear Regression without regularization: “I go along with everything.”
• Lasso: “I’m skeptic at first, but go along with significant trends.”
• Ridge: “I’m easily convinced, but somewhat sluggish.”
• Elastic Net: “I’m feeling somewhere between Ridge and LASSO.”

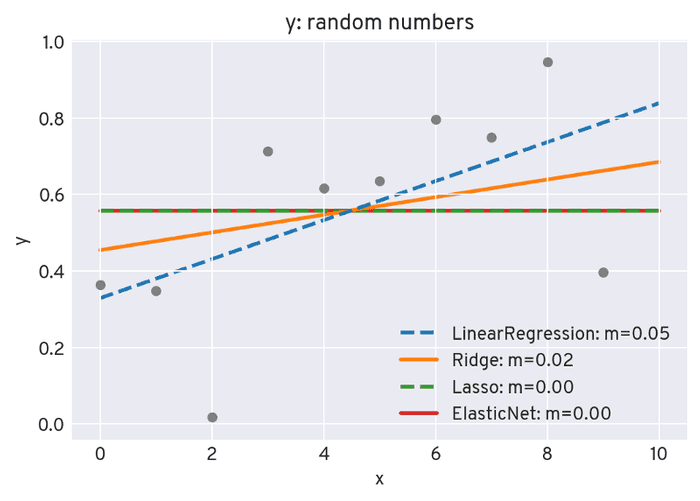
Let’s see what this looks like in practice. For ten random numbers, we’ll perform a linear fit with each of the four methods above (using an increased lambda parameter for Ridge, for demonstration purposes):

Of course, you’ll get a minor random trend in the data, which is unquestioningly picked up by Linear Regression. Ridge regression also picks up the trend, yet weaker. For Lasso and Elastic Net, the linear L1 penalty term is high enough to force the weight (i.e. the slope) to zero when minimizing the loss function.

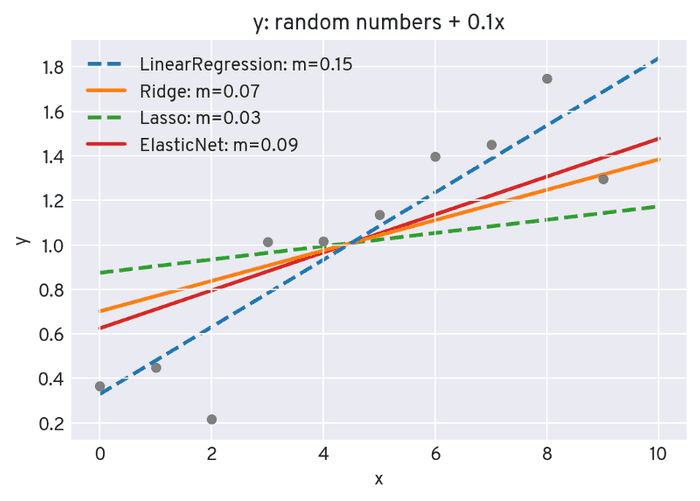
Now, we add a small linear component to the data points and re-run the fitting procedures:

This is already enough for Lasso to not fully “ignore” the slope coefficient anymore.

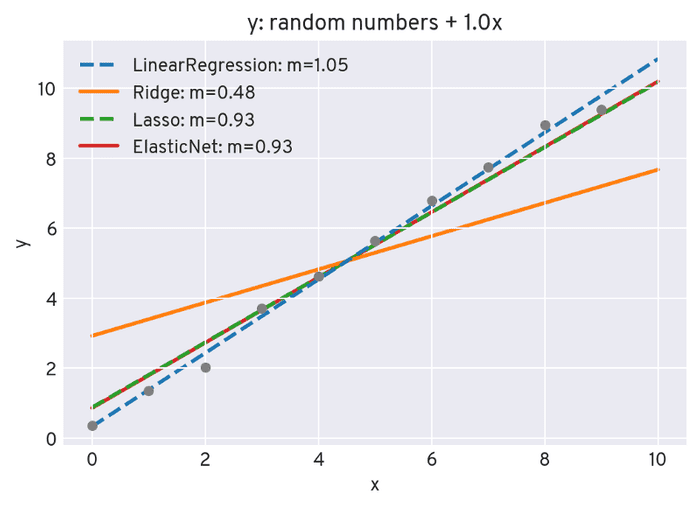
If we further increase the added linear component, we get this:

The Lasso and Elastic Net now almost fully “accept” the significant trend, while for Ridge, the quadratic penalty term leads to a lower slope.

Do you miss anything? Share your opinion or questions in the comments!